Vectores: Un acercamiento no trivial

Este es el primero de una serie de artículos que intentará explicar una de las abstracciones más famosas que se conocen en ciencias e ingeniería conocidas comúnmente como vectores.

Los vectores y las matrices (hablaremos de las matrices en artículos posteriores) forman la médula espinal del álgebra lineal. De estos conceptos divergen una serie de áreas de estudios y aplicaciones como los espacios vectoriales, transformaciones lineales, análisis funcional, ecuaciones diferenciales, teoría de campos, entre otros, en dónde se requiere rigor matemático en los fundamentos de los análisis de algunas magnitudes que necesariamente deben ser tratadas a través de un análisis vectorial para darle un sentido determinante al concepto físico de estudio.

William Hamilton, físico y matemático irlandés (1805-1865), fue el primero en introducir formalidades matemáticas, y elegantes a el desarrollo de la representación vectorial en un plano. A este desarrollo él lo llamó el desarrollo de los cuaterniones. Durante la serie de artículos de este tipo, introduciremos el concepto de cuaterniones.

¿Qué es un vector?

Como definición general, pudiéramos decir que un vector es una abstracción matemática que se puede representar en un plano, para definir un concepto.

Pero debemos ser concretos en lo que decimos, es por ello que no podemos hablar materialmente de vectores si no hablamos de magnitudes. Recurriremos a la física, ´porque en física se estudian magnitudes de fenómenos naturales, esto nos facilitará mucho la “materialización” de la abstracción matemática.

Los fenómenos físicos son medibles. Al ser medibles están relacionados con cantidades y unidades de medida, estos fenómenos físicos medibles, le llamaremos magnitudes físicas.

Existen magnitudes como la temperatura, el tiempo, frecuencia, carga eléctrica, la distancia recorrida, entre otras, que requieren de la especificación de un solo número para la comprensión completa de la magnitud, a estas magnitudes físicas las llamaremos magnitudes escalares. Por otra parte, existen fenómenos físicos que requieren de 2 o más números para especificar completamente la magnitud, como por ejemplo, la velocidad de una partícula desde un punto s a un punto r, no es suficiente con conocer el número que representa la medición absoluta de la velocidad de esta partícula, si no también la dirección en el espacio en dónde se está moviendo la partícula y también el sentido en el que la partícula se dirige en el plano que representa dicho espacio. A este tipo de magnitudes físicas se les conoce como magnitudes vectoriales.

recapitulando todos los conceptos que hemos definido pudiéramos decir concretamente que los vectores materialmente hablando son una abstracción matemática que requieren de una magnitud escalar medible, una dirección y un sentido en el espacio para poder satisfacer la descripción del fenómeno físico.

En estos desarrollos, vamos hablar de vectores de dos y tres dimensiones únicamente, porque es dónde se desarrollan la mayoría de los fenómenos físicos observables sensorialmente, sin embargo, debemos estar anuentes que existen disciplinas mucho más avanzadas como la geometría diferencial y la relatividad general que desarrollan vectores de N dimensiones para la comprensión de un fenómeno.

Enfoque Geométrico de un Vector

Desde el enfoque geométrico, un vector se define como un segmento recto y dirigido en un plano que puede partir desde un punto P hasta un punto Q que denotaremos inicialmente como $\vec{PQ}$, en dónde P es el punto inicial y Q el punto final.

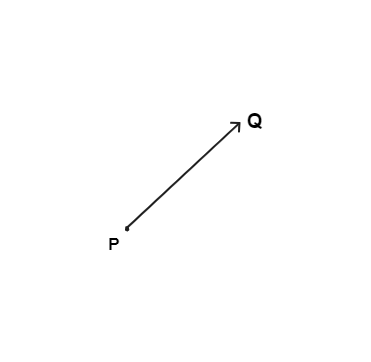
Es usual y práctico representar a un vector con una sola letra, nosotros utilizaremos letras mayúsculas y en negrita para referirnos a los vectores, por ejemplo, al segmento  descrito en la figura 1, le llamaremos vector A para identificarlo.

Definición I:

Un vector en un plano puede interpretarse como un par ordenado de números reales $\langle x,y \rangle$, en dónde los números x e y son las componentes del vector $\langle x,y \rangle$.

De la definición anterior podemos afirmar que puede existir un vector A como un par ordenado $\langle a_1,a_2 \rangle$, si A es un punto en el espacio $(a_1,a_2)$, entonces el vector A, puede representarse geométricamente como un segmento dirigido $\vec{OA}$, donde O, es el origen del plano.

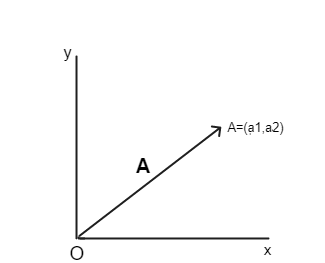
Por ahora, vamos a culminar porque la intención es ir digiriendo poco a poco el marco conceptual antes de ingresar al desarrollo matemático. En el próximo artículo vamos a profundizar aún más sobre el enfoque geométrico de vectores e introduciremos el enfoque algebraico.

Espero que esto haya ayudado a comprender algunas cosas, nos vemos pronto en el siguiente desarrollo, gracias por leer.